TABLE OF CONTENTS The change of coordinates from cartesian (x, y, z) to cylindrical polar (r, ? preserves all of the properties introduced in the previous sections. In fact, any coordinate transformation within the plane perpendicular to the z axis can be performed with the help of the TensorAnalysis package, provided the resulting coordinate system remains orthogonal.
For cylindrical polar coordinates the result has the form
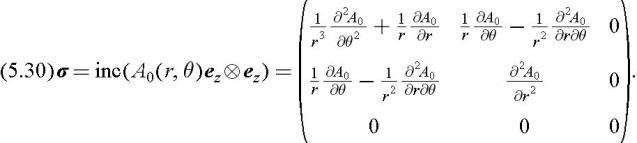
Using MATHEMATICA, the derivation is performed in a few lines.
<b class="bold"><< Tensor2Analysis.m</b><b class="bold">SetCoordinates[Cylindrical[r, t, z]]</b><b class="bold">B = {{0, 0, 0}, {0, 0, 0}, {0, 0, Psi[r, t]}}</b><b class="bold">(Stress1 = Inc [B]) // MatrixForm</b>| Airy stress function | |
|---|---|
| B := {{0, 0, 0}, {0, 0, 0}, {0, 0, A0 [x, y]}} | Airy stress function form of the Beltrami-Maxwell tensor potential B |
